기본 유사 난수 발생과 메르센 트위스터 구현

예제 · 케이플러스 한성탁 · 27 Oct 2017

유사 난수(Pseudo random) 생성 원리

요새는 R을 포함해서 거의 모든 프로그램에 0-1 사이의 난수(Uniform(0,1))를 발생시키는 기능이 포함되어 있습니다. 0-1 사이의 난수는 정규 분포 등을 따르는 다른 난수를 발생시키는 도구로 쓰이기도 하고, 난수를 발생시키기 쉽기 때문입니다. 가장 기본적인 난수라고 할 수 있습니다.

앞에서 난수라고 쓰기는 했는데, 엄밀하게 현재 사용되는 난수들은 정확하게 난수는 아닙니다. 컴퓨터에서 계산을 통해 난수를 발생하고 있는데, 현재 컴퓨터 구조로는 정확한 난수를 발생할 수 없어서 유사(Pseudo) 난수를 사용하고 있습니다. 앞으로 양자컴퓨터가 상용화되면 그때 정확하게 난수를 발생시킬 수 있다고 합니다.

먼저 가장 기본적인 난수 발생 방법을 알아보겠습니다. $X_n$이 발생되어지는 난수들이라고 할 때, 난수들은 다음과 같은 관계식을 가집니다.

$X_{n+1} = (aX_n+c)\;\;mod\;\;m$

이 방법은 Linear congruential generator라고 합니다.(참고:위키피디아)

여기서 $a$는 multiplier, $c$는 increment, $m$은 modulus, $X_0$은 seed라고 하며, $a$, $c$, $X_0$은 모두 m보다 작은 값을 가져야 합니다. 예를 들어 비주얼베이직 6 같은 경우는 $m = 2^{24}$, $a = 43FD43FD_{16}$, $c = C39EC3_{16}$ 입니다.

여기서 seed의 경우 중요한 의미를 가지는데, seed가 동일할 경우 동일한 난수가 생성되기 때문입니다. 이를 통해 seed값을 지정하여 시뮬레이션을 재현하거나, 난수가 사용되는 프로그램의 예제 등에서 같은 결과를 얻거나 할 수 있습니다. R에서는 set.seed() 를 통해 seed를 정할 수 있습니다.

반대로 같은 결과가 나오면 안되는 상황의 경우, 현재 시각이나 날짜 등을 seed로 하여 난수를 발생시키면 seed 문제를 회피할 수 있습니다.

앞에서 설명한 비주얼 베이직의 값으로 난수 생성기를 R로 작성해보았습니다.

m = 2^24
a = 0x43FD43FD
c_ = 0xC39EC3

seed = as.integer(Sys.Date())

generator = function(n, m, a, c_, seed){
  res = numeric(n)
  res[1] = seed
  for(i in 2:n) res[i] = (a * res[i-1] + c_) %% m
  
  return(res / m)
}

u =generator(n = 1000, m = m, a = a, c_ = c_, seed = seed)

plot(u)

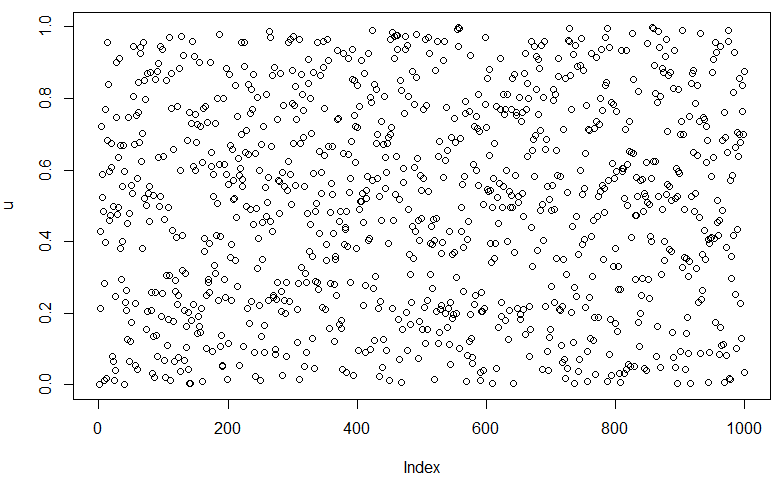
result1

잘 생성되는 것 같습니다.

메르센 트위스터(Mersenne twister)

앞에서 생성한 난수도 사용엔 문제가 없습니다만 현재 프로그램에서 쓰이는 더 정교한 유사 난수 생성기를 소개하겠습니다.

메르센 트위스터는 C++, 엑셀, MATLAB, Python, R 등 여러 프로그램에서 쓰이고 있으며 seed를 포함한 624개의 정수를 이용해서 난수를 생성하게 됩니다. 난수 발생 속도가 빠르고, 메모리를 적게 차지하며, 난수 발생 주기(앞에서 발생시킨 난수와 같은 난수가 발생되는 길이)가 $2^{19937}-1$ 입니다. 참고로 $2^{19937}-1$은 메르센 소수이기 때문에 메르센 트위스터라는 이름을 붙인 것 같습니다.

메르센 트위스터는 발생시키는 난수의 비트 수에 따라 MT19937, MT19937-64로 나뉩니다.

메르센 트위스터의 동작 원리를 간단하게 요약하면 다음과 같습니다.

seed에서 624 크기의 MT 벡터를 생성
MT 벡터를 이용하여 624개의 유사 난수 발생
MT 벡터에 노이즈를 준 후(twist) 2번부터 반복

이론적인 설명과 알고리즘의 자세한 부분은 (링크:위키피디아)를 보시기 바랍니다. 저는 이론적인 부분은 모릅니다만, 위키피디아의 나와있는 슈도 코드를 이용하여 MT19937을 R로 작성해보았습니다. 2^32 이상의 정수에 대해 32비트 부분한 추출하는 함수 bitTrunc32()만 따로 작성하였습니다.

R에서는 시스템적인 문제로 비트연산 패키지가 2^59 정도의 크기까지만 지원하기 때문에 MT19937-64의 구현은 많이 어렵습니다.

require(bit64)
require(bitops)

"%&&%" = function(x, y) bitAnd(x, y)
"%$$%" = function(x, y) bitXor(x, y)
"%<<%" = function(x, y) bitShiftL(x, y)
"%>>%" = function(x, y) bitShiftR(x, y)

n = 624
m = 397

a = 0x9908b0df
f = 0x6c078965


u = 11 ; d = 0xffffffff
s = 7  ; b = 0x9d2c5680
t = 15 ; c = 0xefc60000
l = 18

upper_mask = 0x80000000
lower_mask = 0x7fffffff


index = n+2

bitTrunc32 = function(x){
  if(x <= 0xffffffff) return(x)
  x = as.integer64(x)
  res = c()
  while(x != 0) {
    res = c(res, as.integer(x%%2))
    x = x %/% 2
  }
  y = tail(rev(res), 32)

  sum(y * 2^(31:0))
}

MT = integer(n)

seed_mt = function(seed){
  index <<- n
  MT[1] <<- seed
  for(i in 1:(n-1)){
    MT[i+1] <<- bitTrunc32(f * (MT[i] %$$% (MT[i] %>>% 30)) + 1)
  }
  
  
}

extract_number = function(){
  if(index >= n+1){
    if(index > n+1) error("seed가 생성되지 않았습니다")
    twist()
  }
  
  y = MT[index]
  y = y %$$% ((y %>>% u) %&&% d)
  y = y %$$% ((y %<<% s) %&&% b)
  y = y %$$% ((y %<<% t) %&&% c)
  y = y %$$% (y %>>% l)
  
  index <<- index + 1
  
  bitTrunc32(y)
}


twist = function(){
  for(i in 1:n){
    x = (MT[i] %&&% upper_mask) + (MT[i%%n+1] %&&% lower_mask)
    xA = x %>>% 1
    if(x%%2 != 0) xA = xA %$$% a
    MT[i] <<- MT[(i+m-1)%%n+1] %$$% xA
  } 
  index <<- 1
}

seed_mt(0x12345678)

x = y = numeric(1000)
for(i in 1:1000) x[i] = extract_number()/0xffffffff
for(i in 1:1000) y[i] = extract_number()/0xffffffff

plot(x, y)

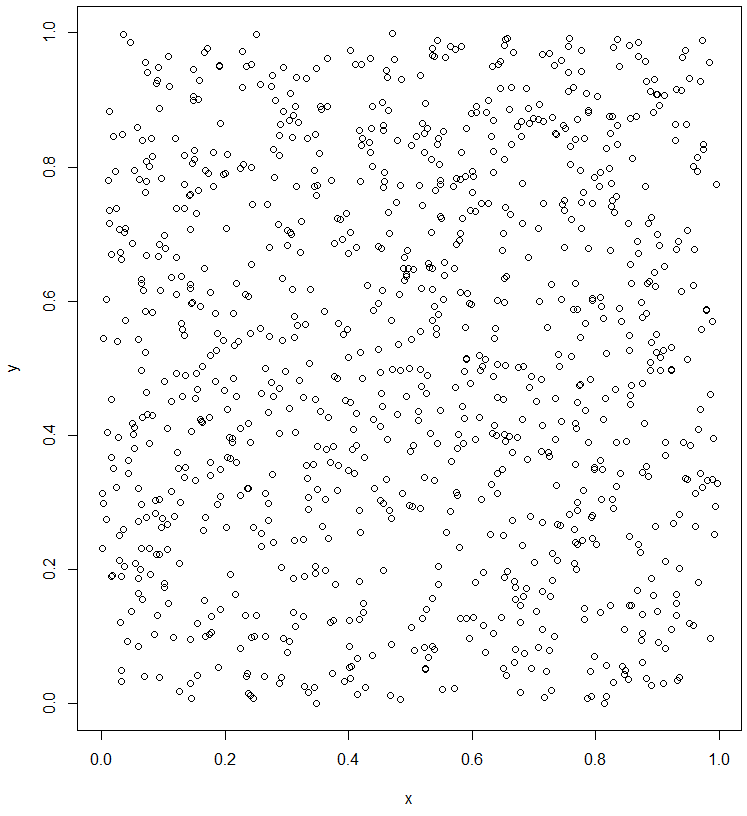
result2

유사 난수가 잘 발생하는 것을 볼 수 있습니다.

추가로 MT19937-64를 julia로 작성해보았습니다. 필요시 참고해주시기 바랍니다.

const w, n, m, r = 32, 624, 397, 31
const a = 0xB5026F5AA96619E9
const u, d = 29, 0x5555555555555555
const s, b = 17, 0x71D67FFFEDA60000
const t, c = 37, 0xFFF7EEE000000000
const l = 43
const f = 0x5851f42d4c957f2d

MT = fill(UInt64(0x0000000000000000), n)

global index = n+2

const lower_mask = 0x7FFFFFFF
const upper_mask = 0x80000000

function seed_mt(seed)
  global index
  index = n + 1
  MT[1] = seed
  for i = 1:(n-1)
    MT[i+1] = f * ( MT[i] $ ( MT[i] >> (w-2) ) ) + i
  end
end

function extract_number()
  global index
  if index >= n + 1
    if index > n + 1
      error("seed가 생성되지 않았습니다")
    end
    twist()
  end

  y::UInt64 = MT[index]
  y = y $ ((y >> u) & d)
  y = y $ ((y << s) & b)
  y = y $ ((y << t) & c)
  y = y $ (y >> l)

  index += 1

  return y
end

function twist()
  global index
  for i = 1:n
    x = MT[i] & upper_mask + (MT[i%n+1] & lower_mask)
    xA = x >> 1

    if x % 2 != 0
      xA = xA $ a
    end

    MT[i] = MT[(i+m-1)%n+1] $ xA
  end
  index = 1
end

seed_mt(0x0000000012345678)

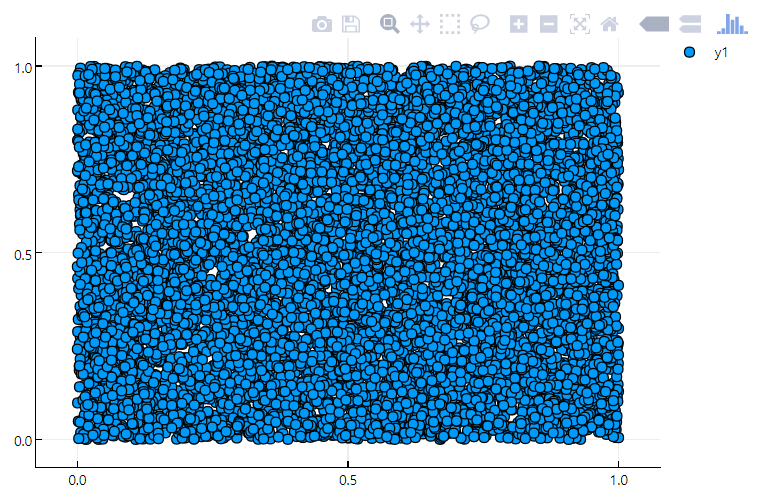
x = [extract_number() / 0xffffffffffffffff for i in 1:10000]
y = [extract_number() / 0xffffffffffffffff for i in 1:10000]

#Pkg.add("Plots")
using Plots
plotly() # Choose the Plotly.jl backend for web interactivity
scatter(x,y)

result3